こんにちは！Takuya.B（@TB_IQ）です。

今日は趣旨を変えて、物理のお話をします。物体が落下する運動はどのように数式で記述することができるのでしょうか？詳しくお話します！

落下運動の物理

今回、物体が自由落下する運動を考えてみます。自由落下運動は初速度0で物体が落ちる運動のことで、手に持ったみかんをそっと床に落とすという状況がまさにそうです。みかんを床に叩きつけて（＝初速度を与える）、みかんがﾌﾞｼｬｰｯしてしまう状況は今回は考えません。

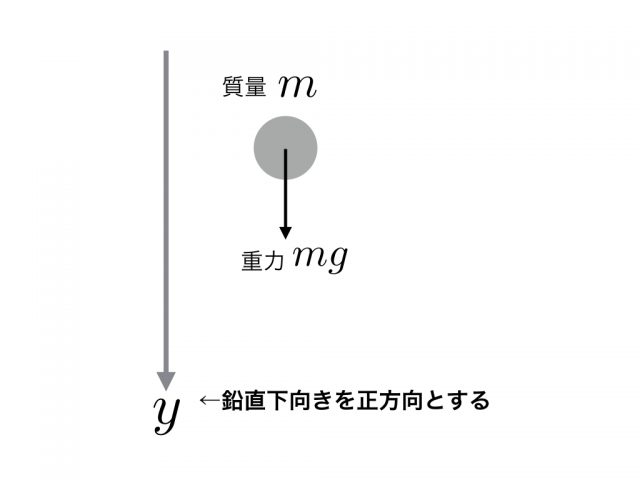
ここで物体に働く力は鉛直下向きの重力$mg$だけ($g$は重力加速度）で、この物体の運動はニュートンの運動方程式を用いて記述することができます。

ニュートンの運動方程式とは次の数式で表されます。

\begin{equation}
\boldsymbol{F}=m\boldsymbol{a} \tag{1}
\end{equation}

ここでFとaは太字ですが、これはベクトルを表しています。ただ、今は1次元($y$軸方向のみ）の運動を考えるので次のように書いて差し支えありません。

\[ F = ma \tag{2} \]

ここで加速度$a$は速度の時間微分（加速度は単位時間あたりの速度の変化）なので、(2)は次のように書くことができます。

\[ F = m \frac{dv}{dt} \tag{3} \]

今、鉛直下向き方向を正としており、力は重力（$F=mg$）のみなので、運動方程式は次のようになります。

\[ m \frac{dv}{dt} = mg  \tag{4} \]

ここで両辺を$m$で割ると、

\[ \frac{dv}{dt} = g \tag{5} \]

今、自由落下運動を考えているので初期条件『時刻$t=0$[$\rm{s}$]のとき速度$v=0$[$\rm{m/s}$]』を考慮して、両辺を定積分すると

\begin{eqnarray}
\int^{v}_{0} dv = g\int^{t}_{0}dt  \\
\\
[v']^{v}_{0} = g[t']^{t}_{0}  \\
\\
v(t) = gt \tag{6}
\end{eqnarray}

となり、速度が求まります。

同様に、速度$v$は位置の時間微分（速度は単位時間あたりの位置の変化）なので、(6)は次のように書くことができます。

\[ \frac{dy}{dt} = gt \tag{7} \]

今、初期値を$y_{0}=0$として、(7)を積分すると

\begin{eqnarray}
\int^{y}_{0} dv = g\int^{t}_{0} t dt  \\
\\
[y']^{y}_{0} = g\left[\frac{1}{2}t^{\prime 2}\right]^{t}_{0}  \\
\\
y(t) = \frac{1}{2}gt^{2} \tag{8}
\end{eqnarray}

となります。ここで重力加速度$g$は $g=9.8$[$\rm{m/s^{2}}$]なので、(8)から、物体が自由落下をはじめて2秒後には約20m落下しているということがわかります。

まとめ

お気付きの方もいらっしゃるかと思いますが、(5)式の段階で両辺を質量$m$で割っているため、これらの結果は質量によりません。つまり、質量が異なっても落下するスピードは同じということです。ビー玉もみかんもボーリングの玉も2秒後には約$20\rm{m}$落下するということです。

ですが、これは普通に考えてありえません。実際は空気抵抗が働きます。空気抵抗が無い(真空)状態で、質量の異なる2つの物体を落下させる実験の動画を見つけたので、ご覧ください。

こういう実験動画って単純に面白いですね！

次回は空気抵抗を考慮した落下運動についてお話します！